precisioninfo.com - Dr Bryan Hall - 2004
The force between any two particles having masses m1 and m2 separated by a distance r is an attraction acting along the line joining the particles and has magnitude
![]()
where G is a universal constant having the same value for all pairs of particles. The present accepted value of G is (Physics - Resnick & Halliday):
![]()
It is a fact of spherical geometry that the gravitational force acting between any two homogeneous spheres having masses m1 and m2 separated by a distance r is exactly as stated for the particulate case.
Exercise
Check that these units of G provide correct units for the force FG
Where we are considering a rocket escaping from the earth we write:
![]()
Where mr denotes the mass of the rocket and me that of the earth
The radius of the earth is stated as 6378.1 kilometres (Google Calculator) and the mass of the earth is reported as 5.9742 × 1024 kilograms (Google Calculator). At the surface of the earth we therefore obtain:
![]()
![]()
![]()
This is the origin of g and note the units of g are exactly as required.
![]()
Further observe g has a representation as ![]() where R is the radius of the earth
where R is the radius of the earth
Note this result does not hold as objects move further away from the surface of the earth.
The force acting on the rocket at all points above the surface of the earth is
![]()
Hence, at all points above the surface of the earth and neglecting friction, the single force acting on the rocket is FG (exactly as shown). From this we can get the rockets acceleration (the rocket is in fact being slowed by gravity so it is deceleration). Writing ar for the acceleration of the rocket and having regard to the consistent use of signs we obtain:
![]()
Exercise:
Apply the representation ![]() to formulate an equivalent expression for ar in terms of g, R and the distance r between the centre of the earth and that of the rocket. The following diagram shows the relationship between R and r. (This problem is substantially solved below where g is inserted into the final velocity expression.)
to formulate an equivalent expression for ar in terms of g, R and the distance r between the centre of the earth and that of the rocket. The following diagram shows the relationship between R and r. (This problem is substantially solved below where g is inserted into the final velocity expression.)
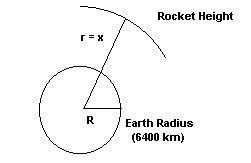
Diagram showing the relationship between R, r & x.
Exercise:
What would be determined on dividing FG by me instead of mr. The answer is not as obvious as you may at first think - particularly in the case where two spheres of equivalent mass are under consideration.
Considering the case only in so far as the rocket is not returning to the earth and changing the separation distance from r to x we can write:
![]()
Þ
![]()
Þ
![]()
Þ
![]()
The initial conditions suggest that, on the surface of the earth (R = 6378.1 km), we have:
![]()
Þ
![]()
Substituting this in we obtain:
![]()
Þ
![]()
Þ
![]()
Þ
(on recalling the representation ![]() )
)
![]()
The rocket will rise for so long as the velocity remains positive; hence we obtain the solution to this problem by setting v = 0
![]()
Þ
![]()
Þ
![]()
Þ
![]()
We obtain the escape velocity by requiring in limiting case x ® ¥ that the expression
![]()
remain positive. That is we require
![]()
Þ
![]()
Þ
![]()
On substituting the values for g and R we obtain the escape velocity vo as:
![]()
Þ
![]()
Converting from metres per second to kilometres per hour yields approximately 40,000 kilometres per hour.